BDM Finite Element

Introduction

The Brezzi-Douglas-Marini (BDM) finite elements have been used to approximate $H(\text{div})$ space, which is used in applications such as linear elasticity and magnetism. In this note, we consider the approximation spaces on a trinagulation of a domain in $\mathbb{R}^2$. Particularly, we consider the BDM${}_1$ space.

BDM elements are approximation to vector spaces (in our case, 2D space). The degrees of freedoms of BDM elements are not associated with vertices because they are not nodal basis functions. To describe the basis functions for BDM${}_1$, consider an edge $E_l = \{z_s, z_t\}, s<t$, then the two BDM${}_1$ basis functions associated with the edge are

\[\phi_{l,1} = \lambda_s \nabla^\bot \lambda_t\qquad \phi_{l,2} = -\lambda_t\nabla^{\bot} \lambda_s\]

For example,

\[\nabla \lambda_2 = \frac{1}{2|K|}\begin{pmatrix}y_3-y_1\\ x_1-x_3\end{pmatrix}\quad \nabla^\bot \lambda_2 = \frac{1}{2|K|}\begin{pmatrix}x_1-x_3\\ y_1-y_3\end{pmatrix}\]

One nice property for $\phi_{l,1}, \phi_{l,2}$ is that for

\[\mathbf{n}_{E_l} = \frac{1}{|E_l|}\begin{pmatrix}y_t-y_s\\ x_s-x_t\end{pmatrix}\]

We have

\[\phi_{l,1}\cdot \mathbf{n}_{E_k}|_{E_k} = \begin{cases} 0 & \text{ if } k\neq l\\ \frac{\lambda_s}{|E_l|} & \text{ if } k = l \end{cases}\qquad \phi_{l,2}\cdot \mathbf{n}_{E_k}|_{E_k} = \begin{cases} 0 & \text{ if } k\neq l\\ \frac{\lambda_t}{|E_l|} & \text{ if } k = l \end{cases}\]

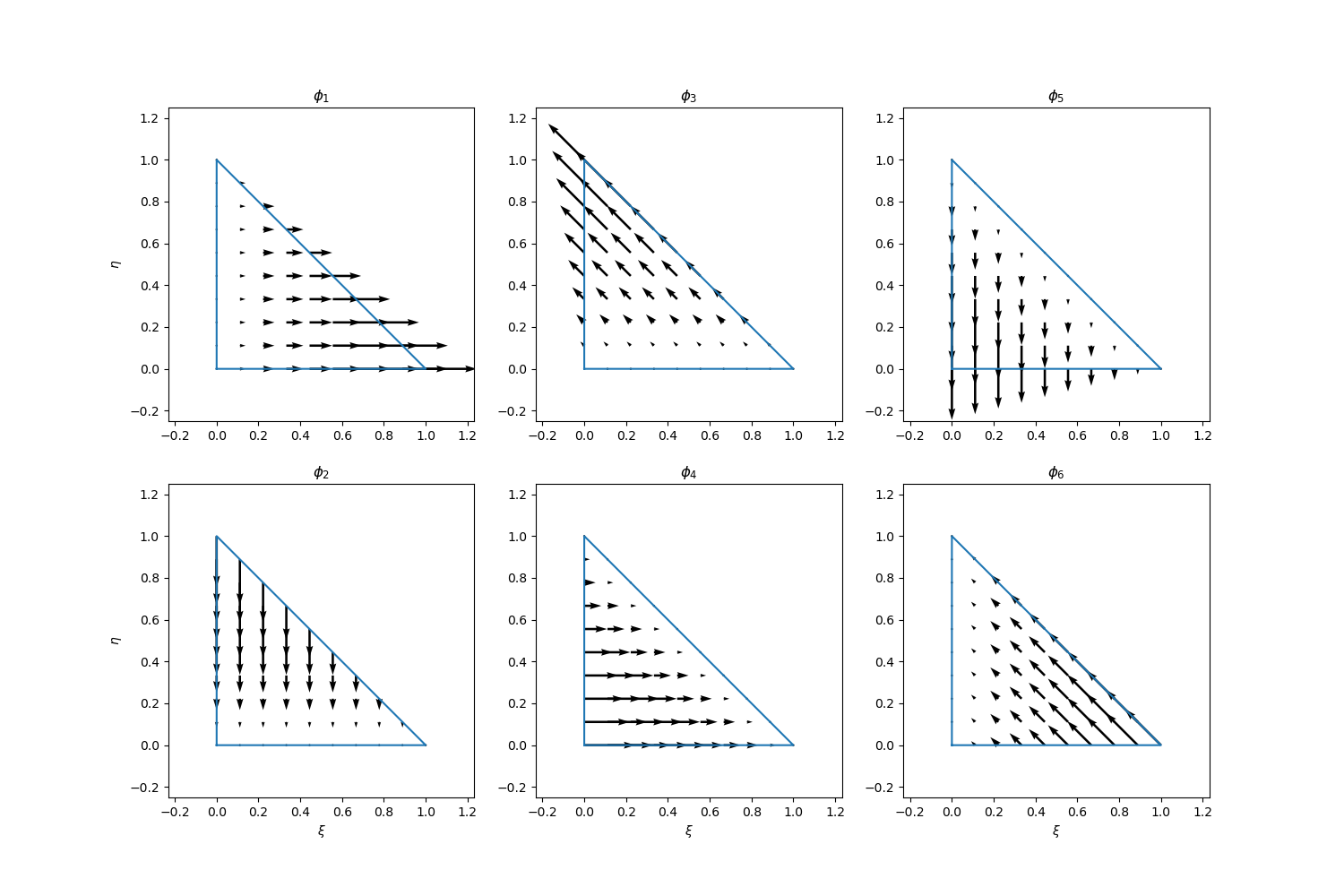
The six basis functions can be visualized as follows (codes are here):

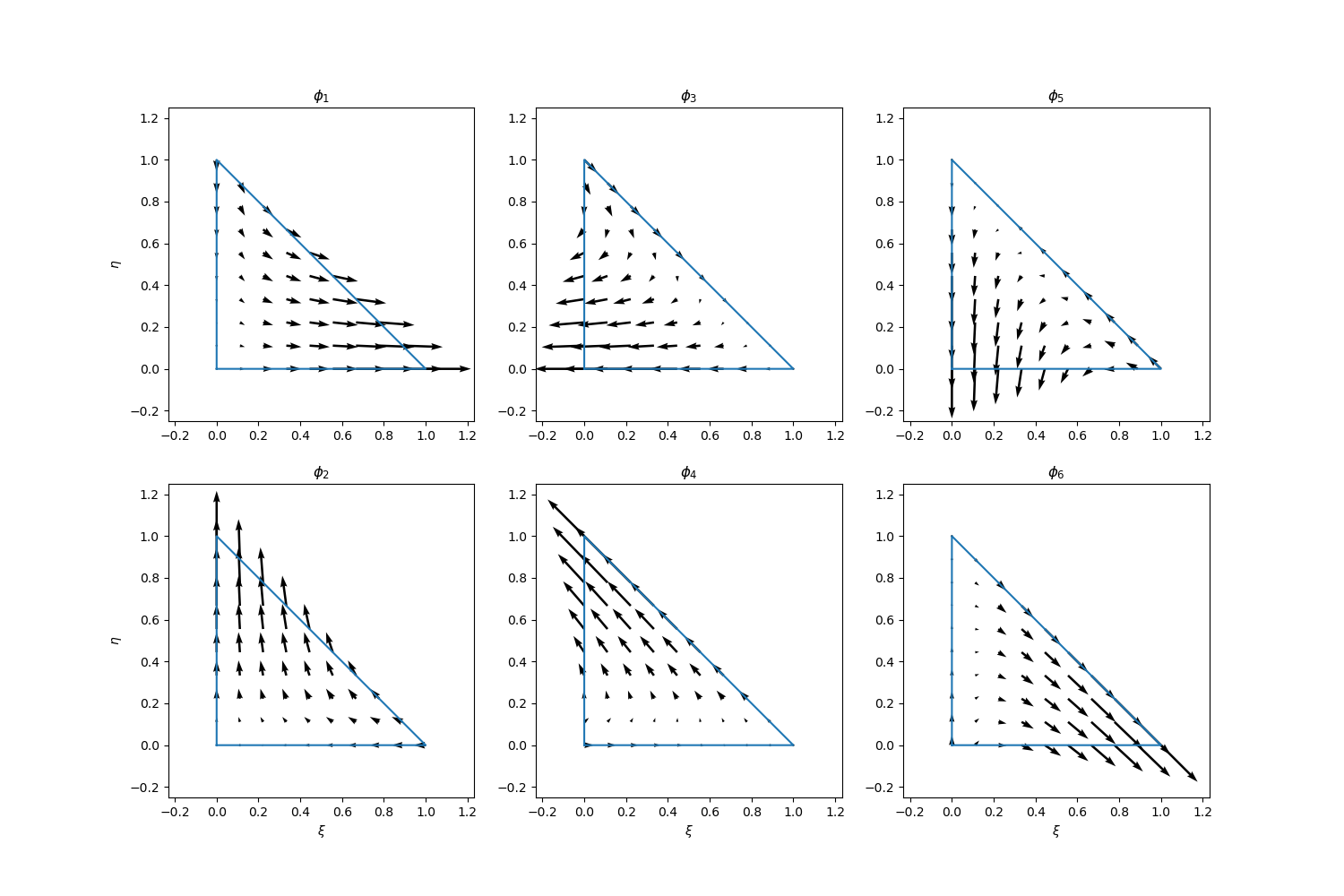
In the finite element calculation, we need to map the reference triangle to the physical one.

Applications

Here are some examples that use BDM${}_1$ elements:

• Poisson's Equation
• Linear Elasticity
• Linear Viscoelasticity